Trong quá trình phân tích dữ liệu, đôi khi một biến độc lập không đủ để giải thích sự thay đổi của biến phụ thuộc. Khi nhiều yếu tố cùng tác động, chúng ta cần một phương pháp có thể xem xét tất cả đồng thời. Hồi quy tuyến tính bội chính là công cụ giúp làm điều đó, cho phép đánh giá mức độ ảnh hưởng của từng biến và dự đoán kết quả một cách rõ ràng. Bài viết dưới đây sẽ giúp bạn hiểu mô hình này và cách thực hiện trên SPSS.
1. Hồi quy tuyến tính bội là gì?
Hồi quy tuyến tính bội (Multiple Linear Regression – MLR) là kỹ thuật thống kê sử dụng nhiều biến độc lập (X₁, X₂, …, Xₙ) để dự đoán một biến phụ thuộc (Y). Đây là phiên bản mở rộng của hồi quy đơn biến, phản ánh đúng bản chất các hiện tượng thực tế — vốn thường chịu tác động từ nhiều yếu tố đồng thời.
Mục tiêu của MLR gồm:
- Mô hình hóa mối quan hệ tuyến tính giữa các biến độc lập và biến phụ thuộc.
- Xác định mức độ tác động của từng biến lên Y khi giữ các biến khác không đổi.

Hồi quy tuyến tính bội là gì?
2. Công thức tổng quát của mô hình MLR
Mô hình hồi quy tổng thể: Y = β0 + β1 X1 + β2 X2 + … + βn Xn + e
Trong đó:
- Y: biến phụ thuộc
- X₁…Xₙ: các biến độc lập
- β₀ (hoặc B₀): hằng số
- βᵢ (hoặc Bᵢ): hệ số hồi quy thể hiện mức thay đổi của Y khi Xᵢ thay đổi một đơn vị
- e: của mô hình
3. Phương pháp ước lượng trong hồi quy tuyến tính bội
Phương pháp bình phương nhỏ nhất (OLS) là phương pháp phổ biến nhất để ước lượng hồi quy tuyến tính. OLS tìm ra đường hồi quy sao cho tổng bình phương phần dư nhỏ nhất. Phần dư là chênh lệch giữa giá trị thực tế và giá trị mô hình dự đoán. Khi đường hồi quy được tối ưu bằng OLS, khoảng cách giữa đường thẳng và các điểm dữ liệu là nhỏ nhất có thể. Do đó, OLS giúp xác định bộ hệ số hồi quy thể hiện tốt nhất xu hướng chung của dữ liệu.
>> Đọc thêm: Lý Thuyết Và Hướng Dẫn Chạy Tương Quan SPSS CHI TIẾT!
4. Các giả định của mô hình hồi quy tuyến tính bội
Để mô hình hoạt động chính xác, MLR phải thỏa các giả định sau:
- Quan hệ tuyến tính: Biến độc lập phải có quan hệ tuyến tính (dạng đường thẳng) với biến phụ thuộc.
- Không đa cộng tuyến mạnh: Các biến độc lập không được tương quan quá cao với nhau.
- Các quan sát độc lập: Dữ liệu cần được thu thập độc lập và ngẫu nhiên.
- Phần dư phân phối chuẩn: Residuals nên phân phối gần chuẩn với trung bình bằng 0.
- Phương sai phần dư không đổi: Phần dư cần có phương sai đồng nhất trên toàn phạm vi giá trị dự đoán.
5. Hướng dẫn thực hiện phân tích hồi quy tuyến tính bội trên SPSS
5.1. Chuẩn bị dữ liệu
Trước khi thực hiện phân tích hồi quy tuyến tính bội trong SPSS, bạn cần phải chuẩn bị dữ liệu cho phù hợp. Các bước cần thực hiện bao gồm:
- Kiểm tra dữ liệu và xử lý dữ liệu thiếu: Kiểm tra dữ liệu đầu vào để đảm bảo rằng chúng không bị sai sót hoặc thiếu sót. Nếu có dữ liệu thiếu, bạn cần xác định nguyên nhân và tiến hành xử lý dữ liệu thiếu bằng cách thay thế giá trị trung bình hoặc giá trị phổ biến của biến.
- Kiểm tra tính đối xứng và phân bố của dữ liệu: Phân tích tính đối xứng và phân bố của các biến để đảm bảo rằng chúng đáp ứng được các giả định phân phối chuẩn trong phân tích hồi quy. Nếu các biến không đáp ứng được giả định này, bạn có thể sử dụng phương pháp biến đổi dữ liệu hoặc biểu đồ (tần số, hộp hoặc phân phối) để kiểm tra tính đối xứng và phân bố của dữ liệu.
5.2. Các bước phân tích hồi quy trong SPSS
Ví dụ: Một nhân viên bán hàng cho thương hiệu xe ô tô A muốn xác định liệu có mối quan hệ giữa thu nhập của cá nhân và giá xe mà họ mua hay không.
- Biến độc lập (Independent): Thu nhập (X₁), Độ tuổi (X₂), Trình độ học vấn (X₃)
- Biến phụ thuộc (Dependent): Giá xe ô tô mà họ phải trả(Y)
Sau khi chuẩn bị dữ liệu, ta thực hiện các bước sau để thực hiện phân tích hồi quy tuyến tính bội trong SPSS:
Bước 1: Khởi tạo mô hình hồi quy tuyến tính trong SPSS
Mở hộp thoại Linear Regression
→ Vào Analyze → Regression → Linear. Đây là nơi bạn khai báo biến phụ thuộc và biến độc lập để chương trình chạy mô hình.
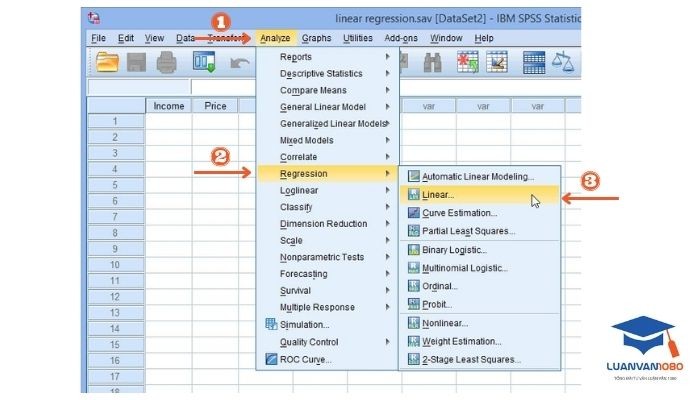
Bước 1: Khởi tạo mô hình hồi quy tuyến tính trong SPSS
Bước 2: Chọn biến phụ thuộc và biến độc lập
Nhập các biến vào ô tương ứng tại hộp thoại Linear Regression:
- Kéo biến phụ thuộc (Giá xe Y) vào ô Dependent. Đây là kết quả hoặc đại lượng bạn muốn dự đoán
- Kéo biến độc lập Thu nhập (X₁), Độ tuổi (X₂), Trình độ học vấn (X₃) vào ô Independent(s). Đây là yếu tố được cho là ảnh hưởng đến biến phụ thuộc
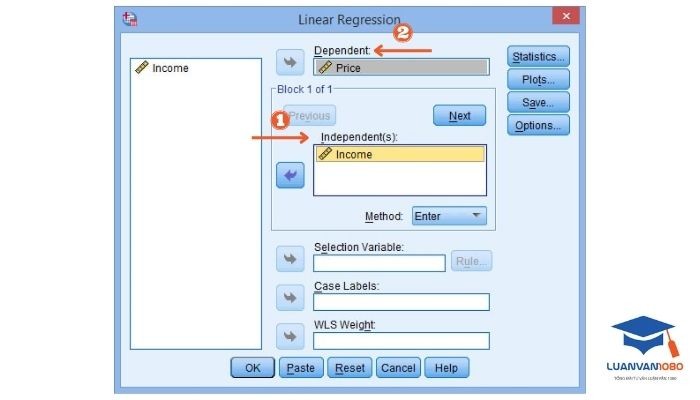
Bước 2: Chọn biến phụ thuộc và biến độc lập trong SPSS
Bước 3: Kiểm tra hiện tượng đa cộng tuyến trong SPSS
Sau khi thực hiện chọn biến phụ thuộc và biến độc lập, bạn click vào (1) Statistics.
Lúc này, cửa sổ “Linear Regression: Statistics” được mở ra. Tiến hành chọn:
- (2) Collinearity: để tính hệ số phóng đại phương sai (VIF).
- (3) Continue: để trở lại hộp thoại Linear Regression.
- Sau đó bấm Continue.
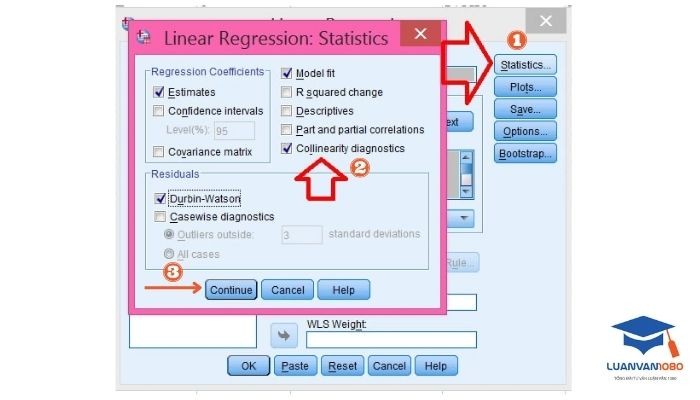
Bước 3: Kiểm tra và đánh giá hiện tượng đa cộng tuyến trong SPSS
Bước 4: Chọn Plots
Nhấn Plots… và thiết lập:
- Kéo ZRESID vào ô Y
- Kéo ZPRED vào ô X
Tích chọn thêm:
- Histogram
- Normal probability plot (P-P Plot)
Nhấn Continue.
Bước 5: Chạy mô hình
Sau khi hoàn tất cài đặt nhấn OK → SPSS sẽ xuất ra các bảng và biểu đồ quan trọng.
>> Tham khảo thêm: Dịch vụ viết thuê luận văn hỗ trợ hoàn thiện nội dung sau khi nộp
5.3. Đọc và giải thích kết quả hồi quy trong SPSS
Đọc bảng ANOVA – kiểm định độ phù hợp mô hình
- Nếu Sig < 0.05 → mô hình phù hợp với dữ liệu.
- Nếu Sig > 0.05 → mô hình không phù hợp.
Đọc bảng Model Summary – đánh giá độ giải thích
Tập trung vào:
- R Square (R²): % biến thiên của Y được giải thích bởi các X.
- Adjusted R Square: độ phù hợp chính xác hơn.
- Durbin–Watson: kiểm tra tự tương quan (1.5–2.5 là chấp nhận).
Đọc bảng Coefficients – đánh giá từng biến
Tại bảng Coefficients, xem:
Sig của từng biến:
- Sig < 0.05 → biến có ý nghĩa thống kê
- Sig > 0.05 → biến không có ý nghĩa
B (hệ số chưa chuẩn hóa): dùng để lập phương trình dự báo.
Beta (hệ số chuẩn hóa): dùng để so sánh mức độ tác động giữa các biến.
VIF: phát hiện đa cộng tuyến (VIF < 10, tốt nhất < 2).
Kiểm định giả định mô hình qua 3 biểu đồ
SPSS tạo ra:
- Histogram phần dư → kiểm tra phân phối chuẩn
- Normal P-P Plot → phần dư bám đường chéo
- Scatter Plot (ZRESID vs ZPRED) → kiểm tra tuyến tính và phương sai hằng định
Nếu các biểu đồ cho kết quả phù hợp, mô hình thỏa giả định hồi quy.
5.4. Viết phương trình hồi quy
Dựa trên kết quả bảng Coefficients ta viết phương trình chuẩn hóa và chưa chuẩn hóa.
Lưu ý:
- Không đưa biến không có ý nghĩa thống kê vào phương trình.
- Luôn giữ phần dư ε cuối phương trình.
- Nếu hệ số âm → phải thể hiện đúng dấu trừ trong phương trình.
Hồi quy tuyến tính bội giúp chúng ta nhìn rõ hơn cách nhiều yếu tố cùng lúc ảnh hưởng đến một kết quả. Khi áp dụng trên SPSS, quá trình phân tích trở nên trực quan và dễ thực hiện hơn, từ việc kiểm tra mô hình đến diễn giải các hệ số. Hiểu và dùng đúng phương pháp này sẽ giúp bạn xử lý dữ liệu tự tin hơn và đưa ra những kết luận có cơ sở rõ ràng trong nghiên cứu cũng như công việc thực tế.


 14 Tháng 1, 2026
14 Tháng 1, 2026 Share
Share











