Phân tích nhân tố khám phá EFA là một phương pháp phân tích định lượng dùng để rút gọn một tập gồm nhiều biến đo lường phụ thuộc lẫn nhau thành một tập biến ít hơn(gọi là các nhân tố) để chúng có ý nghĩa hơn. Cùng Luận văn 1080 tìm hiểu thêm trong bài viết sau đây:

Khái niệm phân tích nhân tố khám phá EFA
1. Giới thiệu về nhân tố khám phá EFA
1.1. Khái niệm EFA
EFA (Exploratory Factor Analysis) là kỹ thuật dùng để kiểm định hai loại biến quan trọng trong thang đo, đó là các giá trị hội tụ và các giá trị phân biệt.
1.2. Phân tích EFA
Phân tích nhân tố khám phá EFA (Exploratory Factor Analysis) là phương pháp thống kê đa biến được sử dụng để tìm ra các mối quan hệ giữa các biến và nhóm các biến tương tự nhau thành các nhóm các yếu tố (factors).
Phân tích nhân tố khám phá EFA được sử dụng để rút gọn một tập hợp k gồm các biến quan sát thành một tập hợp F (với F < k) với các nhân tố có ý nghĩa thống kê:
- Kết quả của phân tích EFA sẽ giúp giảm kích thước của dữ liệu bằng cách tóm tắt các biến liên quan vào các yếu tố, giúp cho việc phân tích và diễn giải dữ liệu trở nên đơn giản hơn.
- Các yếu tố này thường được coi như các biến ẩn, không được đo lường trực tiếp, nhưng có ảnh hưởng đến các biến quan sát.
Trong nghiên cứu: các nhà khoa học thường thu thập số liệu một số lượng biến có cỡ mẫu khá lớn và rất nhiều các biến để quan sát trong đó có quan hệ tương quan lẫn nhau.
- Ví dụ: Thay vì chúng ta đi nghiên cứu 30 đặc điểm nhỏ của một đối tượng thì chúng ta có thể nghiên cứu 5 đặc điểm lớn, trong số mỗi đặc điểm lớn này bao gồm 4 đặc điểm nhỏ có sự tương thích với nhau.
>> Đọc thêm: Nhập Dữ Liệu Từ EXCEL Vào SPSS ĐƠN GIẢN Kèm Ảnh Chi Tiết!
1.3. Khái niệm các nhân tố trong phân tích EFA.
1.3.1. Định nghĩa Factor
Yếu tố Factor trong EFA là yếu tố có các biến có thể quan sát được từ một số đặc điểm chung nào đó mà chúng ta không thể quan sát được trực tiếp. Ví dụ: Factor này có thể được giải thích bằng các khái niệm lớn hơn, như chất lượng cuộc sống, sự hài lòng về công việc, hoặc năng lực quản lý.
Hệ số tải yếu tố (Factor loading)càng cao, nghĩa là có sự tương quan giữa các biến quan sát đó với yếu tố càng lớn và ngược lại.
Mỗi factor (nhân tố) được xác định bởi một tập hợp các biến quan sát được có mối quan hệ cao với nhau và mối quan hệ thấp với các biến khác trong tập dữ liệu. Chúng thường được đo lường bằng phương sai tổng thể giữa các biến quan sát và được liệt kê theo thứ tự gồm các khả năng giải thích của yếu tố đó.
1.3.2. Phương sai (Variance)
Phương sai (Variance) là phép đo lường mức độ chênh lệch giữa các biến giá trị trong một tập dữ liệu.
Trong quá trình đầu tư tài chính, phương sai của lợi nhuận các tài sản trong các danh mục đầu tư được dùng như một phương tiện để phân bố tài sản một cách tốt nhất. Còn trong đầu tư tài chính, phương sai dùng để so sánh sự hiệu quả của các yếu tố trong danh mục đầu tư với nhau và so sánh với các giá trị hiệu suất trung bình.
1.3.3. Hệ số tương quan (Correlation coefficient)
Hệ số tương quan: (Correlation coefficient) là thước đo dùng trong thống kê đo lường mức độ ảnh hưởng mạnh yếu của các mối quan hệ giữa hai biến số. Trong đó:
- Kết quả > 1.0 hoặc nhỏ hơn -1: có lỗi trong quá trình thực hiện phép đo tương quan..
- Kết quả < 0: cho thấy hai biến có mối quan hệ tỉ lệ nghịch với nhau hoặc giá trị tương quan âm (nghịch biến tuyệt đối thể hiện khi mức giá trị bằng -1)
- Kết quả >0 cho thấy có mối quan hệ đồng điều với nhau hoặc mối quan hệ tương quan dương (đồng biến tuyệt đối thể hiện khi mức giá trị bằng 1)
- Kết quả = 0 tức là hai biến sẽ độc lập với nhau.
- Hệ số tương quan có mức từ -1.0 đến 1.0.
Như vậy, ta có thể thấy rằng Factor, Phương sai (Variance) và Hệ số tương quan (Correlation coefficient) đóng một vai trò vô cùng quan trọng trong phân tích nhân tố khám phá EFA.
>> Tham khảo thêm: Dịch vụ viết thuê luận văn kèm tư vấn phương pháp nghiên cứu
2. Mục tiêu và Ứng dụng chạy EFA trong SPSS

Mục tiêu và Ứng dụng chạy EFA trong SPSS
2.1. Mục tiêu
Hai mục tiêu quan trọng của phân tích nhân tố khám phá EFA là kiểm định:
- Số lượng các yếu tố ảnh hướng đến một tập dữ liệu của các biến đo lường.
- Mức độ ảnh hưởng về mối quan hệ giữa mỗi yếu tố với từng biến đo lường.
2.2. Ứng dụng chạy EFA trong SPSS

Ứng dụng của phân tích nhân tố khám phá EFA
- EFA thường được dùng phổ biến trong nhiều lĩnh vực về quản lý, kinh tế – xã hội, tâm lý học,… Khi chúng ta đã có được mô hình khái niệm (Conceptual Framework) từ các giả thuyết hay các nghiên cứu trước đó.
- Trong các nghiên cứu khoa học về ngành kinh tế, các nhà khoa học thường dùng thang đo (scale) bao gồm rất nhiều câu hỏi (biến dùng để đo lường) nhằm đo lường những khái niệm trong mô hình và phân tích nhân tố khám phá EFA sẽ giúp rút gọn một tập gồm rất nhiều biến đo lường thành một số yếu tố.
- Khi có được một số ít các yếu tố, nếu như chúng ta sử dụng các yếu tố này với tư cách là các một biến độc lập trong hàm hồi quy bội thì khi đó mô hình sẽ giảm khả năng xảy ra hiện tượng đa cộng tuyến.
- Bên cạnh đó, các yếu tố được rút ra sau khi phân tích EFA có thể được dùng trong phân tích hồi quy đa biến (Multivariate Regression Analysis), mô hình Logic, sau đó chúng ta có thể tiếp tục sử dụng phân tích nhân tố khẳng định (CFA) để kiểm định độ tin cậy của mô hình hay thực hiện mô hình cấu trúc tuyến tính (Structural Equation Modeling, SEM) để đánh giá về mối quan hệ qua lại phức tạp giữa các biến.
3. Điều kiện để áp dụng phân tích EFA
3.1. Mức độ tương quan giữa các biến đo lường
Phân tích EFA dựa trên mối quan hệ giữa các biến đo lường với nhau. Chính vì vậy, trước khi tiến hành sử dụng phân tích nhân tố khám phá EFA, chúng ta cần kiểm tra xem mối quan hệ giữa các biến đo lường này như thế nào.
Sử dụng ma trận của hệ số tương quan (correlation matrix), chúng ta có thể xác định được mức độ ảnh hưởng giữa các biến. Nếu như các hệ số tương quan có giá trị nhỏ hơn 0.30, khi đó sử dụng phân tích EFA sẽ không phù hợp (Hair et al. 2009)
Bên dưới là một số tiêu chí dùng để đánh giá mối quan hệ giữa các biến:
3.1.1. Kiểm định Bartlett
Kiểm định Bartlett dùng để kiểm tra ma trận tương quan có đúng là ma trận đơn vị (identity matrix) hay không. Ma trận đơn vị ở đây có nghĩa là ma trận có hệ số tương quan giữa các biến bằng 0, và hệ số tương quan với chính nó bằng 1.
Nếu như phép kiểm định Bartlett có giá trị p<5%, chúng ta có thể bác bỏ giả thuyết H0 (ma trận tương quan là một ma trận đơn vị), có nghĩa là các biến dữ liệu có mối quan hệ qua lại với nhau.
3.1.2. Kiểm định KMO
Kiểm định KMO (Kaiser – Meyer – Olkin) là kiểm định dùng để so sánh độ lớn của hệ số tương quan giữa 2 biến Xi và Xj với hệ số tương quan riêng của chúng.
Để sử dụng phân tích EFA, thì kiểm định KMO phải có giá trị lớn hơn 0.50 Kaiser (1974)
- KMO ≥ 0.90: Rất tốt;
- 0.80 ≤ KMO < 0.90: Tốt;
- 0.70 ≤ KMO < 0 80: Được;
- 0.60 ≤ KMO < 0.70: Tạm được;
- 0.50 ≤ KMO < 0.60: Xấu;
- KMO < 0.50: Không chấp nhận được
3.2. Kích thước mẫu
Để sử dụng phân tích nhân tố khám phá EFA, chúng ta cần kiểm định kích thước mẫu lớn, nhưng vấn đề kiểm định kích thước mẫu có phù hợp hay không là việc làm vô cùng phức tạp. Các nhà khoa học thường dựa trên kinh nghiệm nhiều năm của mình.
Trong phân tích EFA, kích thước mẫu thường được kiểm định dựa vào “kích thước tối thiểu” và “số lượng các biến đo lường được đưa vào phân tích EFA”, bên dưới là một số ý kiến, đề xuất từ các nhà khoa học về phân tích nhân tố EFA, các bạn có thể tìm hiểu:
- Hoàng Trọng và Chu Nguyễn Mộng Ngọc (2008), số lượng quan sát các biến (cỡ mẫu) ít nhất phải đạt gấp 4 đến 5 lần số biến trong khi phân tích nhân tố EFA.
- Hair et al. (2009) cho rằng để sử dụng phân tích EFA, kích thước cỡ mẫu tối thiểu phải là 50, tốt nhất nên là 100. Ông Hair đề xuất, cố gắng tối đa hóa tỷ lệ quan sát trên mỗi biến đo lường là 5:1, có nghĩa là cứ 1 biến đo lường thì cần tối thiểu là 5 quan sát.
- Stevens (2002, theo Habing 2003) một yếu tố được xác định là đáng tin cậy nếu như yếu tố này có từ 3 biến đo lường trở lên.
Phân tích, xử lý số liệu là nội dung đòi hỏi người thực hiện phải có đủ kiến thức lẫn kinh nghiệm.
3.3. Biến kiểm soát trong EFA
3.3.1. Khái niệm biến kiểm soát
- Biến kiểm soát (Control Variable) là những biến không phải là biến chính trong nghiên cứu nhưng có thể ảnh hưởng đến mối quan hệ giữa biến độc lập và biến phụ thuộc.
- Nhà nghiên cứu đưa biến này vào mô hình nhằm loại bỏ hoặc giảm thiểu ảnh hưởng của nó, giúp đánh giá chính xác hơn tác động của biến độc lập đến biến phụ thuộc.
3.3.2. Vai trò của biến kiểm soát
- Giảm nhiễu trong phân tích: Hạn chế ảnh hưởng của các yếu tố ngoại lai có thể làm sai lệch kết quả.
- Tăng độ chính xác: Giúp mô hình phản ánh đúng mối quan hệ giữa các biến chính.
- Tăng giá trị khoa học của nghiên cứu: Kết quả có độ tin cậy cao hơn, dễ được công nhận.
3.3.3. Cách kiểm soát biến trong SPSS
- Trong phân tích hồi quy (Regression) hoặc Logistic Regression, ta thêm biến kiểm soát vào mô hình cùng với biến độc lập.
- Điều chỉnh theo biến kiểm soát (covariate) trong phân tích phương sai (ANCOVA)
- Kiểm soát tác động của các yếu tố ngoại lai lên dữ liệu quan sát nhằm loại bỏ biến “nhiễu” trong phân tích nhân tố EFA / CFA.
Vì thế, nếu bạn đang gặp khó khăn trong khi thực hiện trong quá trình nghiên cứu, phân tích và cần đến dịch vụ nhận xử lý số liệu SPSS thì hãy liên hệ ngay với Luận văn 1080 để nhận được sự hỗ trợ nhanh nhất. Chúng tôi luôn có đội ngũ chuyên gia nhiều năm kinh nghiệm luôn sẵn sàng tư vấn, giải quyết khó khăn, giúp bạn tiết kiệm thời gian và nhận được kết quả chất lượng.
4. So sánh giữa EFA và CFA (Confirmatory Factor Analysis)

Phân biệt giữa EFA và CFA
4.1. Giống nhau
Cả hai phân tích đều dùng để đánh giá mối quan hệ giữa các biến quan sát với các biến tiềm ẩn. Qua đó xem xét được biến quan sát nào có ảnh hưởng nhiều nhất vào biến tiềm ẩn mẹ, các biến quan sát nào không có ảnh hưởng.
Cả hai phân tích đều có tính chất hội tụ (convergence) và tính chất phân biệt (discriminant) của các nhóm cấu trúc biến.
4.2. Khác nhau
| Phân tích EFA | Phân tích CFA |
| Thống kê kiểm định thế hệ đầu tiên (truyền thống). | Thống kê kiểm định thế hệ thứ 2 (hiện đại) với đa chức năng và xử lý được nhiều vấn đề mà thống kê thế hệ đầu tiên không xử lý được. |
| Chỉ thiên về khám phá cấu trúc nhân tố. | Chỉ thuần về khẳng định cấu trúc nhân tố. |
| Phân tích EFA là khám phá ra các cấu trúc tiềm ẩn trong một số lượng lớn các biến quan sát nên các nhóm được hình thành sau EFA. | Trong khi đó phân tích CFA luôn cố định xem xét có bao nhiêu cấu trúc biến đó từ xuyên suốt quá trình phân tích, chỉ có loại bỏ đi biết quan sát đã có do biến đó không giải thích được cho biến tiềm ẩn. |
| Các biến khi phân tích đã được chuẩn hóa | Các biến khi phân tích chưa được chuẩn hóa |
| Xác định các biến quan sát đưa vào không có sai số đo lường (dẫn đến ước lượng cho kết quả ít chính xác). | Xác định các biến quan sát đưa vào có sai số đo lường (dẫn đến ước lượng cho kết quả chính xác hơn). |
5. Mô hình phân tích nhân tố khám phá EFA
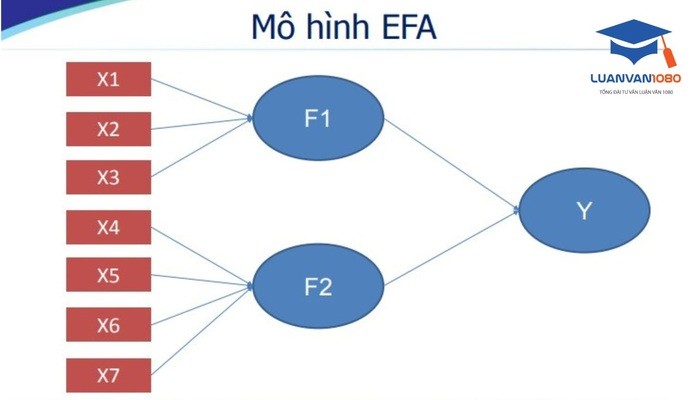
Mô hình phân tích nhân tố khám phá EFA
Trong phân tích nhân tố khám phá EFA, mỗi biến đo lường được biễu diễn như là một tổ hợp tuyến tính của các nhân tố cơ bản, còn lượng biến thiên của mỗi biến đo lường được giải thích bởi những nhân tố chung(common factor).
5.1. Biểu diễn biến đo lường
Biến thiên chung của các biến đo lường được mô tả bằng một số ít các nhân tố chung cộng với một số nhân tố đặc trưng(unique factor) cho mỗi biến. Nếu các biến đo lường được chuẩn hóa thì mô hình nhân tố được thể hiện bằng phương trình:
Xi = Ai1 * F1 + Ai2 * F2 + Ai3 * F3 + . . .+ Aim * Fm + Vi*Ui
Trong đó:
- Xi : biến đo lường thứ i đã được chuẩn hóa
- Aij: hệ số hồi qui bội đã được chuẩn hóa của nhân tố j đối với biến i
- F1, F2, . . ., Fm: các nhân tố chung
- Vi: hệ số hồi qui chuẩn hóa của nhân tố đặc trưng i đối với biến i
- Ui: nhân tố đặc trưng của biến i
5.2. Mối quan hệ giữa nhân tố chung và biến đo lường
Các nhân tố đặc trưng có tương quan với nhau và tương quan với các nhân tố chung; mà bản thân các nhân tố chung cũng có thể được diễn tả như những tổ hợp tuyến tính của các biến đo lường, điều này được thể hiện thông qua mô hình sau đây:
Fi = Wi1*X1 + Wi2*X2 + Wi3*X3 + . . . + Wik*Xk
Trong đó,
- Fi: ước lượng trị số của nhân tố i
- Wi: quyền số hay trọng số nhân tố(weight or factor scores coefficient)
- k: số biến
Trong quá trình phân tích nhân tố EFA, cần đưa các biến kiểm soát vào mô hình giúp kiểm soát các yếu tố ngoại cảnh có thể ảnh hưởng đến kết quả phân tích, đặc biệt là khi thực hiện phân tích trên các dữ liệu quan sát trong thực tế.
Để hiểu rõ hơn các biến kiểm soát có thể có vài trò quan trọng và ảnh hưởng đến quá trình phân tích nhân tố EFA như thế nào, xem ngay biến kiểm soát là gì? – Vai trò và cách kiểm soát biến trong SPSS
6. Các bước thực hiện phân tích nhân tố khám phá EFA
Quy trình thực hiện EFA có thể được trình bày theo nhiều cách và nhiều bước(step) khác nhau, tùy theo quan điểm của từng nhà nghiên cứu:
6.1. Quy trình 6 bước theo Hoàng Trọng & Chu Mộng Ngọc (2010)
Theo Hoàng Trọng và Chu Mộng Ngọc(2010), có 6 bước để thực hiện EFA:
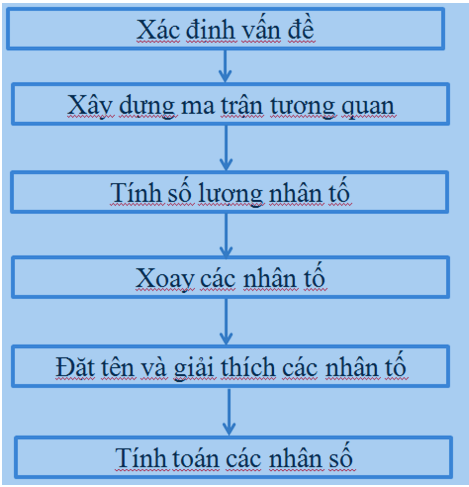
Phân tích nhân tố EFA 6 bước theo Hoàng Trọng & Chu Mộng Ngọc (2010)
6.2. Quy trình 7 bước theo Rietveld & Van Hout (1993)
Theo Rietveld & Van Hout (1993), có 7 bước chính để thực hiện EFA:
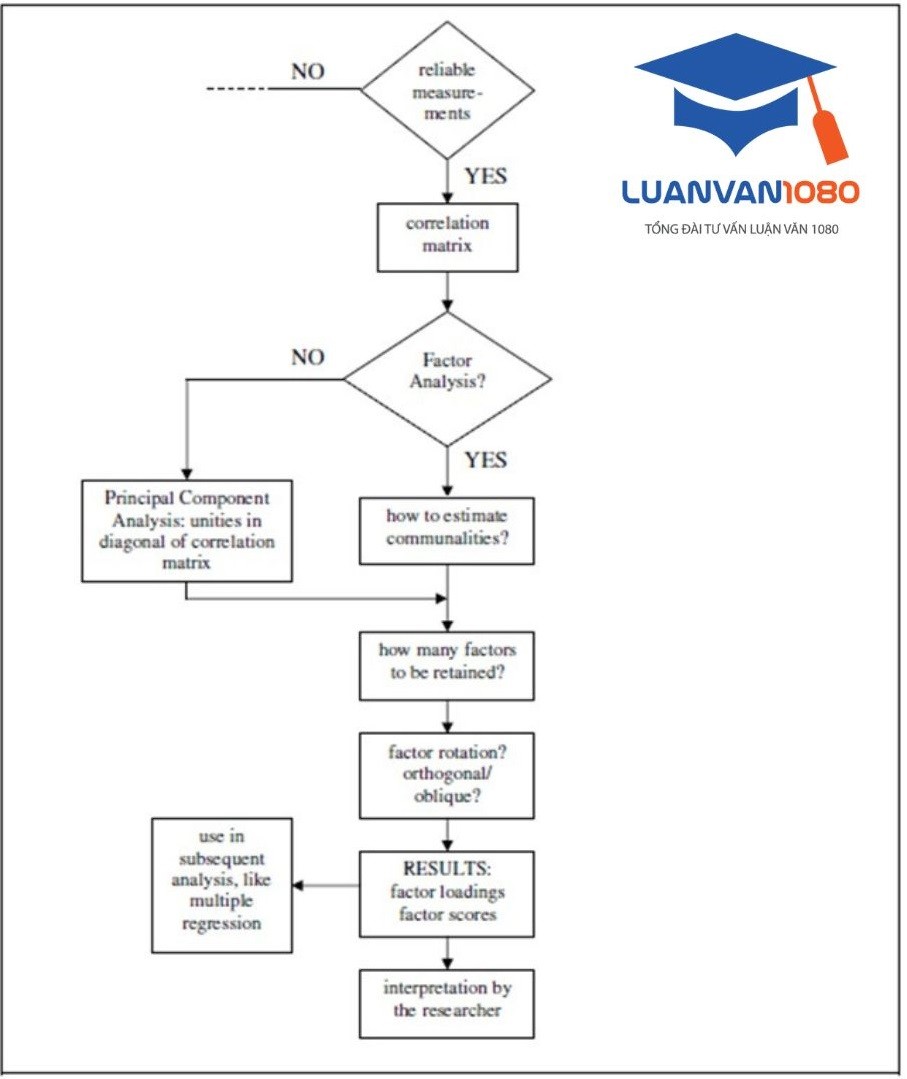
7 bước chính để thực hiện EFA theo Rietveld & Van Hout (1993)
6.3. Quy trình 5 bước theo Williams, Onsman & Brown (2010)
Theo Williams, Onsman, Brown (2010), có 5 bước thực hiện EFA:
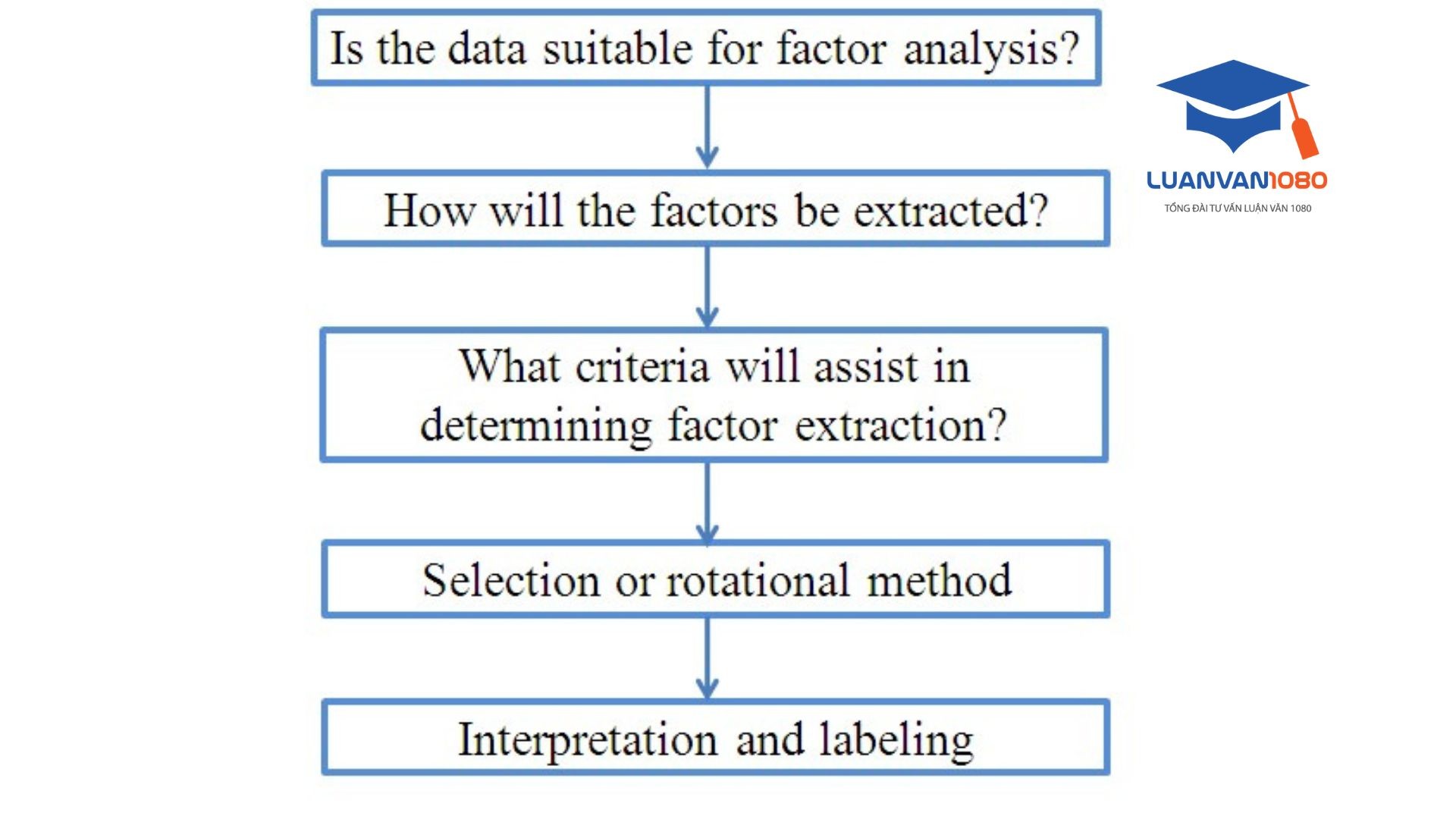
5 bước chính để thực hiện EFA theo Williams, Onsman & Brown (2010)
Phân tích nhân tố EFA và ANCOVA (Analysis of Covariance) là rất quan trọng trong quá trình phân tích dữ liệu. Cả hai phương pháp đều sử dụng biến kiểm soát để kiểm soát ảnh hưởng của các yếu tố khác trong quá trình phân tích.
Tuy nhiên, cách thực hiện và mục đích của hai phương pháp này khác nhau. Xem ngay Ancova là gì? Cách Kiểm Định Ancova trong SPSS tại website Luận văn 1080 để hiểu về chúng và tránh được những sai sót không đáng có trong quá trình tiến hành kiểm định.
7. Các vấn đề cần lưu ý trong phân tích EFA

Các vấn đề cần lưu ý trong phân tích nhân tố khám phá EFA
7.1. Nên dùng biến độc lập hay biến phụ thuộc để phân tích EFA?
- Phân tích EFA thường được áp dụng cho biến độc lập nhằm phát hiện các nhân tố tiềm ẩn có thể giải thích sự biến thiên của các biến này.
- Trong một số trường hợp, EFA có thể áp dụng cho biến phụ thuộc, nhằm kiểm nghiệm các yếu tố ẩn ảnh hưởng đến sự biến thiên của chúng.
- Tuy nhiên, không nên đưa biến độc lập và biến phụ thuộc vào phân tích EFA cùng lúc, đặc biệt khi dùng phép quay vuông góc (orthogonal rotation), bởi điều này có thể làm sai lệch kết quả phân tích tiếp theo (Nguyễn Đình Thọ, 2012).
7.2. Ta nên phân tích EFA chung hay riêng?
- Nếu phân tích EFA riêng cho từng thang đo, kết quả có thể không đạt được giá trị phân biệt tốt nhất (discriminant validity). Do đó, cần cân nhắc khi đánh giá.
- Tuy nhiên, việc phân tích EFA chung cho tất cả các biến độc lập và phụ thuộc không phải là lựa chọn tối ưu, vì hai nhóm biến này thường không có tương quan trực tiếp và mục tiêu phân tích khác nhau.
- Tóm lại: EFA chủ yếu được áp dụng trên biến độc lập để xác định các yếu tố tiềm ẩn. Có thể dùng trên biến phụ thuộc trong một số nghiên cứu, nhưng việc gộp cả hai nhóm biến trong cùng một phân tích EFA thường không mang lại kết quả có ý nghĩa thống kê.
Trong khi học về tóm tắt và trình bày dữ liệu, chắc chắn bạn cần quan tâm đến nội dung xử lý câu hỏi có thể chọn nhiều trả lời. Chúng ta xử lý câu hỏi nhiều lựa chọn trong SPSS như thế nào? Và chúng ta thực hiện thống kê tần số ra sao? là những câu hỏi nhiều người đặt ra khi đề cập đến nội dung này. Tham khảo ngay bài viết tại website Luận văn 1080 của chúng tôi để nhận được câu trả lời chính xác nhất.
Như vậy, bài viết trên đã tổng hợp các khái niệm, mục tiêu, ứng dụng, các điều kiện, mô hình và các bước thực hiện EFA chuẩn nhất. Hy vọng sẽ nắm được tất cả kiến thức trên. Chúc các bạn áp dụng vào bài phân tích thành công!


 14 Tháng 1, 2026
14 Tháng 1, 2026
 Share
Share











